The Birthday Paradox

Hello there! Welcome to the first post on this blog.
In this post, we will understand what is popularly known as “The Birthday Paradox” and along with that, we will look into what this paradox means in cryptography, where the birthday paradox is known as the birthday attack.

Prerequisites

You will need to know the basics of combinatorics & probability theory to understand this article.

Assumptions

For the first part of the article, we also assume that birthdays are distributed uniformly across the year i.e. an equal number of people are born on all days of the year. This assumption is not even close to true, but to begin, it will make it easy to understand the calculations. We will also see what happens when the distribution is not uniform.

The answer

The probability that at least two people have the same birthday with $23$ people is at least $\approx 50\%$ . The reason this is called a paradox is that the number $23$ looks so small compared to the number of days in a year i.e. $365$ days, but still, the probability of at least two people having the same birthday is as high as $\approx50\%$ . These values are calculated with the assumption of uniform distribution and if the distribution is non-uniform, the probability will be higher than $50\%$ .

Next, let’s see how we get this answer. I would highly recommend that you try to solve the problem yourself before you start reading the next section. You can also start reading the solution, and whenever you feel you can do the rest of the process yourself, feel free to stop reading and continue on your own.

Solution

Let’s think of the problem this way, we have $23$ people and we have to assign a birthday between $1$ and $365$ (days of the year) to each of them. We can define the probability that at least two people will share the birthday

$\begin{equation*}= \frac{number\:of\:combinations\:where\:at\:least\:2\:people\:share\:the\:birthday}{total\:number\:of\:possible\:combinations\:of\:birthdays}\end{equation*}$

(We can only use this formula when the probability distribution for the values is uniform.)

For every person, we have $365$ possible values and so the total number of possible combinations of the values that the people can take is $365^{23}$ .

Now, out of these $365^{23}$ combinations, we need the number of combinations where at least two people have the same birthday. To calculate that, we will calculate the number of combinations where no one shares the birthday with anyone else i.e. every person is assigned a different birthday and then subtract this number from the total number of combinations.

Number of combinations where no two people share the birthday $= 365 * 364 * 363 * .. *343$
So, the number of combinations where at least two people share the birthday will be $365^{23} - (365*364*363*...*343)$

Using the above formula, the final probability will be

$\begin{equation*}\begin{align*}&=\frac{365^{23} - (365*364*...*343)}{365^{23}} \\&\approx 0.50729\end{equation*}$

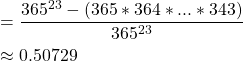
Simple! Wasn’t it? This paradox works because intuitively we try to compare the number of people with the number of days in a year. Instead, we should be comparing the number of possible pairs which is quite high even with relatively fewer people.

But birthdays are not uniform…

We have got the answer to the question we posed, but it works only if the given distribution is uniform. Now, we’ll see what to do if the birthday distribution is not uniform. Let’s start with the notations we will now use:

$N$ – Total number of days
$d_{i}$ – $i^{th}$ day of the year
$p_{i}$ – Probability that a person is born on $d_{i}$
$q$ – Total number of people
$q_{i}$ – $i^{th}$ person from the group
$P(q, N, distribution)$ – Probability that in a group of q people, and considering N days in a year, at least two people will share the birthday for the given distribution

For any probability distribution, data will be given like –

The data will specify the probability that a person is born on that day for every day of the year. In case of uniform distribution, all these probabilities become equal to $\frac{1}{N}$ . Let’s say the name of distribution given to us is $dist$ .

The probability that the $q_{i}$ ‘s birthday lies on a specific day $d_{k}$ is given in the data, say $p_{k}$ . Let’s take another person $q_{j}$ where $i \neq j$ , the probability that $q_{i}$ is born on $d_{k}$ and $q_{j}$ is also born on the same day $d_{k}$ = $p_{k} * p_{k}$ (Because birthday’s are independent)

The probability that the birthday of both the people lie on the same day (any day of the year) = probability for the first day + probability for the second day + … probability for the $N^{th}$ day

$\begin{equation*}\begin{align*}&= (p_{1})^{2} + (p_{2})^{2} + (p_{3})^{2}... + (P_{N})^{2} \\&= p (say)\end{align*}\end{equation*}$

The probability that $q_{i}$ and $q_{j}$ will have the different birthday $= 1-p$

This is the probability that a given pair $(q_{i},\:q_{j})$ have the different birthday.
Total number of pairs in the group of q people

$\begin{equation*}\begin{align*}&= \binom{q}{2} \\&= \frac{q*(q-1)}{2}\end{align*}\end{equation*}$

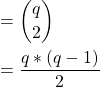
Probability that all the pairs have different birthdays,

$\begin{equation*}\begin{align*}&= (1-p)*(1-p)*(1-p)... \frac{q*(q-1)}{2}\:times \\&= (1-p)^{\frac{q*(q-1)}{2}}\end{align*}\end{equation*}$

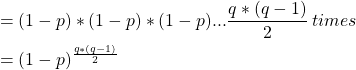
The probability that at least one pair will have the same birthday for the given distribution $dist$ ,

$\begin{equation*}P(q,N,dist) = 1 - (1-p)^{\frac{q*(q-1)}{2}}\end{equation*}$

If we put dist as uniform distribution where $p_{i} = \frac{1}{N}$ for all values of $i$ .

$\begin{equation*}\begin{align*}p &= (p_{1})^{2} + (p_{2})^{2} + (p_{3})^{2}... + (P_{N})^{2} \\p &= \frac{1}{N^{2}} + \frac{1}{N^{2}} + \frac{1}{N^{2}} +... + N times \\p &= N * \frac{1}{N^{2}} \\p &= \frac{1}{N}\end{align*}\end{equation*}$

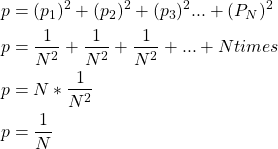
Using the formula derived, for uniform distribution

$\begin{equation*}P(q,N,"uniform") = 1 - (1 - \frac{1}{N})^{\frac{q*(q-1)}{2}}\end{equation*}$

Which will yield the same answer as before for $q = 23$ and $N = 365$ i.e. $\approx0.50729$
Let’s see the graph for different values of $q$ and $N = 365$

Observations

1. The probability that at least two people will have the same birthday is $\approx 1$ with just 70 people in the group.
2. The probability that at least two people will have the same birthday is minimum if the birthday distribution is uniform. For a non-uniform distribution, the probability is higher. This comes with the fact that value of $p$ will be minimum if $p_{1} = p_{2} = p_{3}...p_{N} = \frac{1}{N}$ (Proof here)
3. If we put $q = 1.2*\sqrt{N}$ then, the value of $P(q,N)$ will be $\approx50\%$ in case of uniform distribution

The third observation is a bit non-trivial and works on certain approximations. Let’s work it out.

For large values of q,

$\begin{equation*}\frac{q*(q-1)}{2} \approx \frac{q^{2}}{2}\end{equation*}$

For small values of x,

$\begin{equation*}1 - x \approx e^{-x}\end{equation*}$

Using these approximations, for uniform distribution,

$\begin{equation*}P(q,N) = 1 - e^{\frac{q^{2}}{2*N}} \\\end{equation*}$

Putting $q = 1.2*\sqrt{N}$ ,

$\begin{equation*}\begin{align*}P(q,N) &\approx 1 - e^{-0.72} \\P(q,N) &\approx 0.51325\end{align*}\end{equation*}$

This is what we saw in the above case as well i.e. for $N=365$ , $q = 1.2 * \sqrt{365} \approx 22.926 \approx 23$ , we get the probability very close to $50\%$ . This has some implications in the real world and we will see one next.

Breaking the hash function

In cryptography, the birthday paradox is used to analyze the time complexity of the generic attack to find the collisions for a hash function. The final aim is to find two inputs which will have the same output for the given hash function. The generic attack is to keep evaluating the hash function on different inputs until we find a collision. What will be the time complexity of this attack?
Assuming that the hash function outputs $b$ bits, the total number of possible outputs for the function $= 2^{b}$
By the pigeonhole principle, by evaluating the function at $2^{b}+1$ different inputs, we will find a collision for the hash function with probability $1$ . According to this analysis, the time complexity to find a collision will be $O(2^{b})$ .

Now, If we compare this problem with the birthday paradox we discussed above, we can compare the inputs to the hash function with the people and compare the outputs of the hash function with the birthdays. As per our observation above, if we evaluate the function at $\approx 1.2 * \sqrt{2^{b}}$ values, we will be able to find a collision with the probability $\frac{1}{2}$ .
So, if we evaluate the function at $\approx 1.2 * \sqrt{2^{b}}$ different inputs in a single iteration to find the collision with probability $\frac{1}{2}$ , the expected number of iterations required to find a collision will be $\frac{1}{\frac{1}{2}} = 2$ .
And so the time complexity to find a collision for a given hash function will be $O(\sqrt(2^{b}) = O(2^{\frac{b}{2}})$ which shows the significant reduction in the number of function evaluations we will need to make to find a collision for a given hash function.

Thank you for reading 🙂

References

1. Jonathan Katz and Yehuda Lindell. 2007. Introduction to Modern Cryptography (Chapman & Hall/Crc Cryptography and Network Security Series). Chapman & Hall/CRC.
2. How to prove the sum of squares is minimum?
3. Birthday Problem on Wikipedia

Prerequisites

Assumptions

The answer

Solution

But birthdays are not uniform…

Observations

Breaking the hash function

References

About the author

Akshay Jain

Add Comment

Cancel reply

Akshay Jain

Get in touch