Three may keep a secret, if two of them are dead
Benjamin Franklin
Well, I don’t know a lot about people keeping secrets, but I’m quite sure we want to keep our messages secret when we are sending them to someone else. In this article, we will go through the topic of perfect secrecy which is a fundamental topic in cryptography.
Prerequisites
- The terms used in the context of encryption like ciphertext, encryption key, keyspace, etc.
- Properties of the “exclusive or” operation commonly known as XOR operation.
Brute force
If an attacker intercepts any message encrypted using modern encryption algorithms like Advanced Encryption Standard (AES), the only way for the attacker to break the encryption without knowing the key is to try out all possible keys and figure out which key is the correct one. This is known as the brute force attack.
But how will the attacker figure out which key decrypted the ciphertext correctly? Theoretically, the attacker will see if the decrypted text looks like plain English (in the case of English text) and if it does, the current key is the correct key. The time taken to try out all the keys depends on the computational power available to the attacker. The higher the computational power available, the shorter is the time taken to try out all the keys.
So, is there a way to encrypt your messages so that no one else can decrypt it without the secret key, even if the attacker has infinite computational power? If we can achieve this, we will be able to encrypt the message and be sure that no one else will be able to read them. In other words, we will get the perfect secrecy.
Really?
In practice, the encryption with standard algorithms is considered safe, because with current technology, it will take the attacker hundreds of years to try out all the keys for modern encryption algorithms like AES-256 which uses a 256 bits encryption key. As we progress with better technology, we need to increase the key size as well to make sure that it is not possible to try out all possible keys in a short amount of time. Before AES we had Data Encryption Standard (DES) which was using the key size of 56 bits. With a regular computer, it is possible to try out all 2 ^{56} keys in just a few hours and hence DES is no longer secure.
One-time pad
Perfect secrecy is possible and it is straightforward as well. Let’s start with the simplest and most famous technique that ensures perfect secrecy called one-time pad. The algorithm is a simple one and is based on the properties of the exclusive-or (xor) operation.
Encryption
![]()
where,
Decryption
![]()
Proof of correctness
Let’s see what the decryption evaluates to-
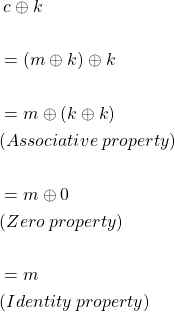
That’s it! This simple algorithm ensures that the encrypted message is safe, and no one can decrypt it without the key even if someone has infinite computational power.
Why not try all keys?
Say, you encrypted the message “flowers” with some secret key, and the output is “xefwrxw”. Now, the attacker will try to decrypt it by trying out every possible key.
| key | decrypted text |
| xgfzvju | academy |
| xfxaeza | absence |
| ejnoehz | hfisnkd |
| mvtizpa | promise |
| jmxozlj | mission |
| annkrky | djioanc |
| bbuhfoa | explore |
| aikaeza | defence |
| … | … |
Just like this, the attacker will see every possible combination of 7 letter words in the decrypted text. There is no way for the attacker to know which one is the correct decryption. In other words, just by looking at the ciphertext, an attacker can’t figure out any detail about the plain text. The attacker still knows as much as he knew before looking at the ciphertext.
Well, this has to be too good to be true. Right? An encryption algorithm so simple and ensures perfect secrecy. Let’s talk about the sad part.
Limitations
The length of the key is at least the length of the message
Claude Shannon proved that for any algorithm to provide perfect secrecy, the length of the key has to be greater than or equal to the size of the original message. So, if you want to encrypt a 1000 bit message, you need at least 1000 bit long key to encrypt it. If you already have a way to share such a long secret key securely, then why not use that to send the message itself.
Proof
In the case of the one-time pad, the attacker can try out all possible keys but can’t figure out which one is the correct one. The reason for this is the attacker will see all the possible values in the message space when trying out all keys and hence we said that the attacker knows nothing about the original message. If the attacker doesn’t see all the possible messages in the decrypted text after trying out all the keys, the attacker would know that the original message is one of the decrypted messages and will be able to discard some messages in the message space. So, the attacker got to know something about the original plaintext after looking at the ciphertext and that violates our perfect secrecy requirement.
In case, the key length is lesser than the message length, the possible number of keys will be lesser than the possible number of messages. And if the attacker tries all the keys, the number of decrypted messages will be equal to the number of possible keys, which is lesser than the number of possible messages. So, the attacker was able to discard some of the messages in the message space.
The argument might come that the key needs to equal to message length and we may use the same key to encrypt multiple messages but that’s not true either.
One time use
We can not use the same key to encrypt two messages, and this is the reason the algorithm was named the one-time pad. This limitation is specific to the one-time pad algorithm but is generally true for other perfectly secret encryption algorithms. For the one-time pad, if the same key is used to encrypt two different messages, the security of both the messages will break.
Proof
If two messages ![]() and
and ![]() are encrypted using the same key
are encrypted using the same key ![]() and
and ![]() and
and ![]() are the corresponding ciphertexts.
are the corresponding ciphertexts.
![]()
If the attacker gets to know

So, the attacker gets to know the xor of the two plain text messages. With this the attacker get’s to know exactly where the two plain messages differ and because the attacker now knows about the plain texts, the algorithm is no longer perfect secure.
Truly random key
The encryption key should be a truly random string i.e. they key should be picked randomly from a uniform probability distribution which is a very difficult task to perform using just software.
Proof
If the keyspace is not uniformly distributed, the attacker will know which keys are more likely to be selected and hence which of the decrypted messages are more likely to be correct given a specific ciphertext. Again, the attacker knows something (which plaintexts are more likely) about the original plaintext after looking at the ciphertext and hence it can’t be perfectly secure.
Uniform mapping
This one is intuitive to see from the above example on the one-time pad. We saw that if the ciphertext is decrypted using all possible keys, we get all the messages in the message space. This must be true for all algorithms with perfect secrecy. If this is not true, the attacker will be able to discard some of the messages in the message space and hence the algorithm will not be perfectly secure.
Because of these limitations, the one-time pad or any other algorithm which can provide perfect secrecy is not practical to use.
Final words
The question comes – are these algorithms useless then? The answer is No. We can still use the one-time pad or similar algorithms to ensure security in case of critical data. Consider a scenario where you and your friend want to share some information secretly over a public channel. What you can do is share a very long secret key when you meet in person, and then you can use that key to share messages up to the length of the key shared originally. This allows you to share the key before you actually send the sensitive message.
Further reading
- SIGSALY was used in WWII to send secret messages and it used the one-time pad as the encryption mechanism
https://en.wikipedia.org/wiki/SIGSALY - Moscow-Washington hotline used the one-time pad algorithm for the encryption of the communication
https://en.wikipedia.org/wiki/Moscow%E2%80%93Washington_hotline - How an attacker can use the xor of two plain text messages
https://stackoverflow.com/questions/5670287/cryptanalysis-xor-of-two-plaintext-files